Записывается тройной интеграл так:

Вычислить тройной интеграл - значит найти число, равное объёму тела V или, что то же самое - области V .

Практически каждый может понять смысл вычисления тройного интеграла "на своей шкуре". Точнее - "под шкурой", а ещё точнее - по своим органам дыхания - лёгким. Вне зависимости от того, знаете ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол - пузырьковых образований, оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так: объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое "огромное количество малостей" математически как раз и формулируется понятие тройного интеграла.

Почему именно тройной интеграл служит для нахождения объёма тела V ? Пусть область V разбита на n произвольных областей Δv i , причём под этим обозначением подразумевается не только каждая маленькая область, но и её объём. В каждой такой маленькой области выбрана произвольная точка M i , а f (M i ) - значение функции f (M ) в этой точке. Теперь будем максимально увеличивать число таких маленьких областей, а наибольший диаметр Δv i - наоборот, уменьшать. Можем составить интегральную сумму вида

Если функция f (M ) = f (x , y , z ) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом .

В этом случае функция f (M ) = f (x , y , z ) называется интегрируемой в области V ; V - областью интегрирования; x , y , z - переменными интегрирования, dv (или dx dy dz ) - элементом объёма.

Вычисление тройного интеграла путём уменьшения кратности

Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.

Рассмотрим трёхмерную область V . Снизу и сверху (то есть по высоте) эта область ограничена поверхностями z = z 1 (x , y ) и z = z 2 (x , y ) . С боковых сторон (то есть по ширине) область ограничена поверхностями y = y 1 (x ) и y = y 2 (x ) . И, наконец, по глубине (если Вы смотрите на область в направлении оси Ox ) - поверхностями x = a и x = b

Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область V была правильной. Она правильна тогда, когда прямая, параллельная оси Oz , пересекает границу области V не более чем в двух точках. Правильными трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже - прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.

Чтобы наглядно представить отличие правильности от неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На рисунке ниже - пример неправильной области V - однополостный гиперболоид, поверхность которого прямая, параллельная оси Oz (красного цвета), пересекает более чем в двух точках.

Мы будем рассматривать только правильные области.

Итак, область V - правильная. Тогда для любой функции f (x , y , z ) , непрерывной в области V , справедлива формула

Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению внутреннего определённого интеграла по переменной z (при постоянных x и y ) и внешнего двойного интеграла по двумерной области D .

Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:

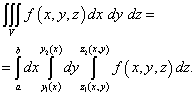
Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.

Вычисляются эти интегралы от самого внутреннего (по переменной z ) к самому внешнему (по переменной x ). Для удобства восприятия последовательности вычислений три "вложенных" интеграла можно записать так:

.

Из этой записи уже однозначно видно, что:

• сначала нужно интегрировать функцию f (x , y , z ) по переменной z , а в качестве пределов интегрирования взять уравнения z = z 1 (x , y ) и z = z 2 (x , y ) поверхностей ограничивающих область V снизу и сверху;
• y y = y 1 (x ) и y = y 2 (x ) поверхностей, ограничивающих область V с боковых сторон;
• получившийся на предыдущем шаге результат интегрировать по переменной x , а в качестве пределов интегрирования взять уравнения x = a и x = b поверхностей, ограничивающих область V по глубине.

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу

-

последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.

Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:

.

Вычислим второй интеграл - по переменной y :

.

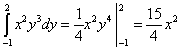x :

.

Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.

Пример 2. Вычислить тройной интеграл

,

где V - параллелепипед, ограниченный плоскостями x = − 1 , x = + 1 , y = 0 , y = 1 , z = 0 , z = 2 .

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:

.

z

.

Вычисляем интеграл "в серединке" - по переменной y . Получаем;

.

Теперь вычисляем самый внешний интеграл - по переменной x :

Ответ: данный тройной интеграл равен -2.

Пример 3. Вычислить тройной интеграл

,

где V x + y + z = 1 и координатными плоскостями x = 0 , y = 0 , z = 0 . Область V проецируется на плоскость xOy в треугольник D , как показано на рисунке ниже.

Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0 . Чтобы получить верхний предел, выразим z из x + y + z = 1 . Получаем 1 − x − y . Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0 . Для получения верхнего предела выразим y из x + y + z = 1 , считая при этом, что z = 0 (так как линия расположена в плоскости xOy ). Получаем: 1 − x .

Сводим данный тройной интеграл к последовательности трёх определённых интегралов:

.

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

.

y . Получаем:

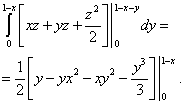
x :

Ответ: данный тройной интеграл равен 1/8.

Вычислить тройной интеграл самостоятельно, а затем посмотреть решение

Пример 4. Вычислить тройной интеграл

,

где V - пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0 , y = 0 , z = 0 .

Расстановка пределов интегрирования при переходе к последовательности трёх интегралов

Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность. В первом примере область интегрирования V представляла собой параллелепипед, с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно заданы уравнениями плоскостей. Во втором примере - пирамида: здесь уже требовалось чуть больше подумать и выразить один из пределов из уравнения. А если область V ограничивают не плоские поверхности? Нужно, конечно, определённым образом осмотреть область V .

Начнём с примера "пострашнее", чтобы почувствовать "обстановку, приближенную к боевой".

Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V - эллипсоид

.

Решение. Пусть центр эллипсоида - начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу. Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена ниже плоскости xOy z и полученное выражение со знаком минус будет нижним пределом интегрирования по переменной z :

.

Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy . Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z :

.

Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:

Чтобы получить нижний предел интегрирования по переменной y , нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:

.

Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:

Что касается интегрирования по переменной x , то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a : x 1 = − a и x 2 = a .

Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:

,

где "игрек первое", "игрек второе", "зет первое" и "зет второе" - полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc /3 .

Следующие примеры - не такие страшные, как только что рассмотренный. При этом они предполагают не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте, чему вы научились, следя за решением "страшного" примера. Думать при расстановке пределов всё равно придётся.

Пример 6. Вычислить тройной интеграл

если область интегрирования ограничена плоскостями x + y = 1 , x + 2y = 4 , y = 0 , y = 1 , z = 1 , z = 5 .

Решение. "Курортный" пример по сравнению с примером 5, так как пределы интегрирования по "игрек" и "зет" определены однозначно. Но придётся разобраться с пределами интегрирования по "иксу". Проекцией области интегрирования на плоскость xOy является трапеция ABCD .

В этом примере выгоднее проецировать трапецию на ось Oy , иначе, чтобы вычислить тройной интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по "иксу" чисто алгебраически. Для этого выразим "икс" из первого и второго уравнений, данных в условии примера. Из первого уравения получаем нижний предел 1 − y , из второго - верхний 4 − 2y . Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

.

Внимание! В этом примере самый внешний интеграл - не по переменной "икс", а по переменной "игрек", а "средний" - по переменной "икс"! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox , на на ось Oy .

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

Вычисляем средний интеграл - по переменной x . Получаем:

.

Наконец, вычисляем самый внешний интеграл - по переменной y :

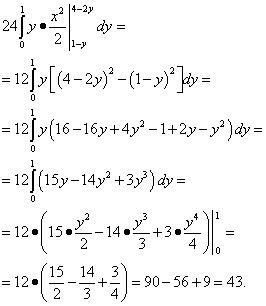
Ответ: данный тройной интеграл равен 43.

Пример 7. Вычислить тройной интеграл

,

если область интегрирования ограничена поверхностями x = 0 , y = 0 , z = 2 , x + y + z = 4 .

Решение. Область V (пирамида MNRP ) является правильной. Проекцией области V на плоскость xOy является треугольник AOB .

Нижние пределы интегрирования по всем переменным заданы в условии примера. Найдём верхний предел интегирования по "иксу". Для этого выразим "икс" из четвёртого уравнения, считая "игрек" равным нулю, а "зет" равным двум. Получаем x = 2 . Найдём верхний предел интегирования по "игреку". Для этого выразим "игрек" из того же четвёртого уравнения, считая "зет" равным двум, а "икс" - переменной величиной. Получаем y = 2 − x . И, наконец, найдём верхний предел интегрирования по переменной "зет". Для этого выразим "зет" из того же четвёртого уравнения, считая "игрек" и "зет" переменными величинами. Получаем z = 4 − x − y .

Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

.

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

.

Вычисляем средний интеграл - по переменной y . Получаем:

.

Вычисляем самый внешний интеграл - по переменной x и окончательно находим данный тройной интеграл:

Ответ: данный тройной интеграл равен 2.

Замена переменных в тройном интеграле и цилиндрические координаты

Если проекцией области интегрирования на какую-либо из координатных плоскостей является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами (r , φ , z ), где r - расстояние от начала координат до проекции N точки M на плоскость xOy , φ - угол между вектором ON и положительным направлением оси Ox , z - аппликата точки M (рисунок ниже).

Прямоугольные координаты x , y , z с цилиндрическими координатами r , φ , z связывают формулы

x = r cosφ ,

y = r sinφ ,

z = z .

Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r , φ , z :

То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:

Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:

Пример 8. Вычислить тройной интеграл

переходом к цилиндрическим координатам, где V - область, ограниченная поверхностями и .

Решение. Так как область V на плоскость xOy проектируется в круг , то координата φ изменяется в пределах от 0 до 2π , а координата r - от r =0 до r =1. Постоянному значению в пространстве соответствует цилиндр . Рассматривая пересечение этого цилиндра с областью V , получаем изменение ординаты z от z = r ² до z = 1 . Переходим к цилиндрическим координатам и получаем.

Пусть имеем две прямоугольные системы координат в пространстве и
, и систему функций

(1)

которые устанавливают взаимно-однозначное соответствие между точками некоторых областей
и
в этих системах координат. Предположим, что функции системы (1) имеют в
непрерывные частные производные. Определитель, составленный из этих частных производных

,

называют якобианом (или определителем Якоби) системы функций (1). Мы будем предполагать, что
в
.

В сделанных выше предположениях имеет место следующая общая формула замены переменных в тройном интеграле:

Как и в случае двойного интеграла, взаимная однозначность системы (1) и условие
могут нарушаться в отдельных точках, на отдельных линиях и на отдельных поверхностях.

Система функций (1) каждой точке
ставит в соответствие единственную точку
. Эти три числа
называют криволинейными координатами точки. Точки пространства
, для которых одна из этих координат сохраняет постоянное значение, образуют т.н. координатную поверхность.

II Тройной интеграл в цилиндрических координатах

Цилиндрическая система координат (ЦСК) определяется плоскостью
, в которой задана полярная система координат и осью
, перпендикулярной этой плоскости. Цилиндрическими координатами точки
, где
– полярные координаты точки– проекции точкина плоскость
, а– это координаты проекции точкина ось
или
.

В плоскости
введем обычным образом декартовы координаты, ось аппликат направим по оси
ЦСК. Теперь нетрудно получить формулы, связывающие цилиндрические координаты с декартовыми:

(3)

Эти формулы отображают областьна все пространство
.

Координатными поверхностями в рассматриваемом случае будут:

1)
– цилиндрические поверхности с образующими, парал-лельными оси
, направляющими которых служат окружности в плоскости
, с центром в точке;

2)

;

3)
– плоскости, параллельные плоскости
.

Якобиан системы (3):

.

Общая формула в случае ЦСК принимает вид:

Замечание 1 . Переход к цилиндрическим координатам рекомендуется в случае, когда область интегрирования – это круговые цилиндр или конус, или параболоид вращения (или их части), причем ось этого тела совпадает с осью аппликат
.

Замечание 2. Цилиндрические координаты можно обобщить так же, как и полярные координаты на плоскости.

Пример 1. Вычислить тройной интеграл от функции

по области
, представляющей собой внутреннюю часть цилиндра
, ограниченную конусом
и параболоидом
.

Решение. Эту область мы уже рассматривали в §2, пример 6, и получили стандартную запись в ДПСК. Однако, вычисление интеграла в этой области затруднительно. Перейдем в ЦСК:

.

Проекция
тела
на плоскость
– это круг
. Следовательно, координатаизменяется от 0 до
, а– от0 до R . Через произвольную точку
проведем прямую, параллельную оси
. Прямая войдет в
на конусе, а выйдет на параболоиде. Но конус
имеет в ЦСК уравнение
, а параболоид
– уравнение
. Итак, имеем

III Тройной интеграл в сферических координатах

Сферическая система координат (ССК) определяется плоскостью
, в которой задана ПСК, и осью
, перпендикулярной плоскости
.

Сферическими координатами точки пространства называют тройку чисел
, где– полярный угол проекции точки на плоскость
,– угол между осью
и вектором
и
.

В плоскости
введем декартовы координатные оси
и
обычным образом, а ось аппликат совместим с осью
. Формулы, связывающие сферические координаты с декартовыми таковы:

(4)

Эти формулы отображают область на всё пространство
.

Якобиан системы функций (4):

.

Координатные поверхности составляют три семейства:

1)
– концентрические сферы с центром в начале координат;

2)
– полуплоскости, проходящие через ось
;

3)
– круговые конусы с вершиной в начале координат, осью которых служит ось
.

Формула перехода в ССК в тройном интеграле:

Замечание 3. Переход в ССК рекомендуется, когда область интегрирования – это шар или его часть. При этом уравнение сферы
переходит в. Как и ЦСК, рассмотренная ранее, ССК «привязана» к оси
. Если центр сферы смещён на радиус вдоль координатной оси, то наиболее простое сферическое уравнение получим при смещении вдоль оси
:

Замечание 4. Возможно обобщение ССК:

с якобианом
. Эта система функций переведет эллипсоид

в «параллелепипед»

Пример 2. Найти среднее расстояние точек шара радиуса от его центра.

Решение. Напомним, что среднее значение функции
в области
– это тройной интеграл от функции по области деленный на объём области. В нашем случае

Итак, имеем

Процедура вычисления тройного интеграла аналогична соответствующей операции для двойного интеграла. Для ее описания введем понятие правильной трехмерной области:

Определение 9.1. Трехмерная область V, ограниченная замкнутой поверхностью S, называется правильной, если:

1. любая прямая, параллельная оси Оz и проведенная через внутреннюю точку области, пересекает S в двух точках;
2. вся область V проектируется на плоскость Оху в правильную двумерную область D;
3. любая часть области V, отсеченная от нее плоскостью, параллельной какой-либо из координатных плоскостей, обладает свойствами 1) и 2).

Рассмотрим правильную область V, ограниченную снизу и сверху поверхностями z=χ(x,y) и z=ψ(x,y) и проектирующуюся на плоскость Оху в правильную область D, внутри которой х изменяется в пределах от а до b, ограниченную кривыми y=φ1(x) и y=φ2(x) (рис.1). Зададим в области V непрерывную функцию f(x, y, z).

Определение 9.2. Назовем трехкратным интегралом от функции f(x, y, z) по области V выражение вида:

Трехкратный интеграл обладает теми же свойствами, что и двукратный. Перечислим их без доказательства, так как они доказываются аналогично случаю двукратного интеграла.

Вычисление тройного интеграла.

Теорема 9.1. Тройной интеграл от функции f(x,y,z) по правильной области V равен трехкратному интегралу по той же области:

. (9.3)

Доказательство.

Разобьем область V плоскостями, параллельными координатным плоскостям, на п правильных областей . Тогда из свойства 1 следует, что

где – трехкратный интеграл от функции f(x,y,z) по области .

Используя формулу (9.2), предыдущее равенство можно переписать в виде:

Из условия непрерывности функции f(x,y,z) следует, что предел интегральной суммы, стоящей в правой части этого равенства, существует и равен тройному интегралу . Тогда, переходя к пределу при , получим:

что и требовалось доказать.

Замечание.

Аналогично случаю двойного интеграла можно доказать, что изменение порядка интегрирования не меняет значения трехкратного интеграла.

Пример. Вычислим интеграл где V - треугольная пирамида с вершинами в точках (0, 0, 0), (1, 0, 0), (0, 1, 0) и (0, 0, 1). Ее проекцией на плоскость Оху является треугольник с вершинами (0, 0), (1, 0) и (0, 1). Снизу область ограничена плоскостью z = 0, а сверху - плоскостью x + y + z = 1. Перейдем к трехкратному интегралу:

Множители, не зависящие от переменной интегриро-вания, можно вынести за знак соответствующего интеграла:

Криволинейные системы координат в трехмерном пространстве.

1. Цилиндрическая система координат.

Цилиндрические координаты точки Р(ρ,φ,z) - это полярные координаты ρ, φ проекции этой точки на плоскость Оху и аппликата данной точки z (рис.2).

Формулы перехода от цилиндрических координат к декартовым можно задать следующим образом:

x = ρ cosφ, y = ρ sinφ, z = z. (9.4)

1. Сферическая система координат.

В сферических координатах положение точки в пространстве определяется линейной координатой ρ - расстоянием от точки до начала декартовой системы координат (или полюса сферической системы), φ - полярным углом между положительной полуосью Ох и проекцией точки на плоскость Оху, и θ - углом между положительной полуосью оси Оz и отрезком OP (рис.3). При этом

Зададим формулы перехода от сферических координат к декартовым:

x = ρ sinθ cosφ, y = ρ sinθ sinφ, z = ρ cosθ. (9.5)

Якобиан и его геометрический смысл.

Рассмотрим общий случай замены переменных в двойном интеграле. Пусть в плоскости Оху дана область D, ограниченная линией L. Предположим, что х и у являются однозначными и непрерывно дифференцируемыми функциями новых переменных u и v:

x = φ(u, v), y = ψ(u, v). (9.6)

Рассмотрим прямоугольную систему координат Оuv, точка Р΄(u, v) которой соответствует точке Р(х, у) из области D. Все такие точки образуют в плоскости Оuv область D΄, ограниченную линией L΄. Можно сказать, что формулы (9.6) устанавливают взаимно однозначное соответствие между точками областей D и D΄. При этом линиям u = const и

v = const в плоскости Оuv будут соответствовать некоторые линии в плоскости Оху.

Рассмотрим в плоскости Оuv прямоугольную площадку ΔS΄, ограниченную прямыми u = const, u+Δu = const, v = const и v+Δv = const. Ей будет соответствовать криволинейная площадка ΔS в плоскости Оху (рис.4). Площади рассматриваемых площадок тоже будем обозначать ΔS΄ и ΔS. При этом ΔS΄ = Δu Δv. Найдем площадь ΔS. Обозначим вершины этого криволинейного четырехугольника Р1, Р2, Р3, Р4, где

P1(x1, y1), x1 = φ(u, v), y1 = ψ(u, v);

P2(x2, y2), x2 = φ(u+Δu, v), y2 = ψ(u+Δu, v);

P3(x3, y3), x3 = φ(u+Δu, v+Δv), y3 = ψ(u+Δu, v+Δv);

P4(x4, y4), x4 = φ(u, v+Δv), y4 = ψ(u, v+Δv).

Заменим малые приращения Δu и Δv соответствующими дифференциалами. Тогда

При этом четырехугольник Р1 Р2 Р3 Р4 можно считать параллелограммом и определить его площадь по формуле из аналитической геометрии:

(9.7)

Определение 9.3. Определитель называется функциональным определителем или якобианом функций φ(х, у) и ψ(х, у).

Переходя к пределу при в равенстве (9.7), получим геометрический смысл якобиана:

то есть модуль якобиана есть предел отношения площадей бесконечно малых площадок ΔS и ΔS΄.

Замечание. Аналогичным образом можно определить понятие якобиана и его геометрический смысл для п-мерного пространства: если x1 = φ1(u1, u2,…,un), x2 = φ2(u1, u2,…,un),…, xn = φ(u1, u2,…, un), то

(9.8)

При этом модуль якобиана дает предел отношения «объемов» малых областей пространств х1, х2,…, хп и u1, u2,…, un .

Замена переменных в кратных интегралах.

Исследуем общий случай замены переменных на примере двойного интеграла.

Пусть в области D задана непрерывная функция z = f(x,y), каждому значению которой соответствует то же самое значение функции z = F(u, v) в области D΄, где

F(u, v) = f(φ(u, v), ψ(u, v)). (9.9)

Рассмотрим интегральную сумму

где интегральная сумма справа берется по области D΄. Переходя к пределу при , получим формулу преобразования координат в двойном интеграле.

Преобразование двойного интеграла от прямоугольных координат ,к полярным координатам
, связанных с прямоугольными координатами соотношениями
,
, осуществляется по формуле

Если область интегрирования
ограничена двумя лучами
,
(
), выходящими из полюса, и двумя кривыми
и
, то двойной интеграл вычисляют по формуле

.

Пример 1.3. Вычислить площадь фигуры, ограниченной данными линиями:
,
,
,
.

Решение. Для вычисления площади области
воспользуемся формулой:
.

Изобразим область (рис. 1.5). Для этого преобразуем кривые: , , , . Перейдем к полярным координатам: , . . В полярной системе координат область описывается уравнениями:

.

1.2. Тройные интегралы

Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.

В декартовых координатах тройной интеграл обычно записывают так:

.

Если
, то тройной интеграл по областичисленно равен объему тела:

.

Вычисление тройного интеграла

Пусть область интегрирования ограничена снизу и сверху соответственно однозначными непрерывными поверхностями
,
, причем проекция областина координатную плоскость
есть плоская область
(рис. 1.6).

Тогда при фиксированных значениях соответствующие аппликатыточек областиизменяются в пределах. Тогда получаем: . Если, кроме того, проекция определяется неравенствами , , где - однозначные непрерывные функции на , то

.

Пример 1.4. Вычислить
, где- тело, ограниченное плоскостями:

	, , , ( , , ). Решение. Областью интегрирования является пирамида (рис. 1.7). Проекция области есть треугольник , ограниченный прямыми , , (рис. 1.8). При аппликаты точек удовлетворяют неравенству , поэтому .
	Расставляя пределы интегрирования для треугольника , получим

Тройной интеграл в цилиндрических координатах

При переходе от декартовых координат
к цилиндрическим координатам
(рис. 1.9), связанных с
соотношениями
,
,
, причем

	, ,, тройной интеграл преобразуется: Пример 1.5. Вычислить объем тела, ограниченного поверхностями: , , . Решение. Искомый объем тела равен .
	Областью интегрирования является часть цилиндра, ограниченного снизу плоскостью , а сверху плоскостью (рис. 1.10). Проекция областиесть круг с центром в начале координат и единичном радиусом. Перейдем к цилиндрическим координатам. , , . При аппликаты точек , удовлетворяют неравенству или в цилиндрических координатах:

Область
, ограниченная кривой
, примет вид, или
, при этом полярный угол
. В итоге имеем

.

2. Элементы теории поля

Напомним предварительно способы вычисления криволинейных и поверхностных интегралов.

Вычисление криволинейного интеграла по координатам от функций, определенных на кривой , сводится к вычислению определенного интеграла вида

если кривая задана параметрическии
соответствует начальной точке кривой, а
- ее конечной точке.

Вычисление поверхностного интеграла от функции
, определенной на двусторонней поверхности, сводится к вычислению двойного интеграла, например, вида

,

если поверхность , заданная уравнением
, однозначно проецируется на плоскость
в область
. Здесь- угол между единичным вектором нормалик поверхностии осью
:

.

Требуемая условиями задачи сторона поверхности определяется выбором соответствующего знака в формуле (2.3).

Определение 2.1. Векторным полем
называется векторная функция точки
вместе с областью ее определения:

Векторное поле
характеризуется скалярной величиной –дивергенцией:

Определение 2.2. Потоком векторного поля
через поверхность называется поверхностный интеграл:

,

где - единичный вектор нормали к выбранной стороне поверхности, а
- скалярное произведение векторови.

Определение 2.3. Циркуляцией векторного поля

по замкнутой кривой называется криволинейный интеграл

,

где
.

Формула Остроградского-Гаусса устанавливает связь между потоком векторного поля через замкнутую поверхность и дивергенцией поля:

где - поверхность, ограниченная замкнутым контуром , а - единичный вектор нормали к этой поверхности. Направление нормали должно быть согласовано с направлением обхода контура .

Пример 2.1. Вычислить поверхностный интеграл

,

где - внешняя часть конуса
(
), отсекаемая плоскостью
(рис 2.1).

Решение. Поверхность однозначно проецируется в область
плоскости
, и интеграл вычисляется по формуле (2.2).

Единичный вектор нормали к поверхности найдем по формуле (2.3): . Здесь в выражении для нормали выбран знак плюс, так как угол между осью и нормалью- тупой и, следовательно, должен быть отрицательным. Учитывая, что , на поверхностиполучаем

Область
есть круг
. Поэтому в последнем интеграле переходим к полярным координатам, при этом
,
:

Пример 2.2. Найти дивергенцию и ротор векторного поля
.

Решение. По формуле (2.4) получаем

Ротор данного векторного поля находим по формуле (2.5)

Пример 2.3. Найти поток векторного поля
через часть плоскости:
, расположенную в первом октанте (нормаль образует острый угол с осью
).

	Решение. В силу формулы (2.6) . Изобразим часть плоскости : , расположенную в первом октанте. Уравнение данной плоскости в отрезках имеет вид (рис. 2.3). Вектор нормали к плоскости имеет координаты: , единичный вектор нормали
	. . , , откуда , следовательно,

где
- проекция плоскостина
(рис. 2.4).

Пример 2.4. Вычислить поток векторного поля через замкнутую поверхность, образованную плоскостью
и частью конуса
(
) (рис. 2.2).

Решение. Воспользуемся формулой Остроградского-Гаусса (2.8)

.

Найдем дивергенцию векторного поля по формуле (2.4):

где
- объем конуса, по которому ведется интегрирование. Воспользуемся известной формулой для вычисления объема конуса
(- радиус основания конуса,- его высота). В нашем случае получаем
. Окончательно получаем

.

Пример 2.5. Вычислить циркуляцию векторного поля
по контуру , образованному пересечением поверхностей
и
(
). Проверить результат по формуле Стокса.

Решение. Пересечением указанных поверхностей является окружность
,
(рис. 2.1). Направление обхода выбирается обычно так, чтобы ограниченная им область оставалась слева. Запишем параметрические уравнения контура :

откуда

причем параметр изменяется отдо
. По формуле (2.7) с учетом (2.1) и (2.10) получаем

.

Применим теперь формулу Стокса (2.9). В качестве поверхности , натянутой на контур , можно взять часть плоскости
. Направление нормали
к этой поверхности согласуется с направлением обхода контура . Ротор данного векторного поля вычислен в примере 2.2:
. Поэтому искомая циркуляция

где
- площадь области
.
- круг радиуса
, откуда

Скачать с Depositfiles

Тройной интеграл.

Контрольные вопросы.

Тройной интеграл, его свойства.

Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.

Вычисление тройного интеграла в сферических координатах.

Пусть функция u = f (x,y ,z ) определена в ограниченной замкнутой области V пространства R 3 . Разобьём область V произвольным образом наn элементарных замкнутых областей V 1 , … , V n , имеющих объемы  V 1 , …,  V n соответственно. Обозначим d – наибольший из диаметров областей V 1 , … , V n . В каждой области V k выберем произвольную точку P k (x k , y k , z k )и составим интегральную сумму функции f (x , y , z )

S =

Определение. Тройным интегралом от функции f (x , y , z ) по области V называется предел интегральной суммы
, если он существует.

Таким образом,

(1)

Замечание. Интегральная сумма S зависит от способа разбиения области V и выбора точек P k (k =1, …, n ). Однако, если существует предел, то он не зависит от способа разбиения области V и выбора точек P k . Если сравнить определения двойного и тройного интегралов, то легко увидеть в них полную аналогию.

Достаточное условие существования тройного интеграла. Тройной интеграл (13) существует, если функция f (x , y , z ) ограничена в V и непрерывна в V , за исключением конечного числа кусочно-гладких поверхностей, расположенных в V .

Некоторые свойства тройного интеграла.

1) Если С – числовая константа, то

3) Аддитивностьпо области. Если область V разбита на области V 1 и V 2 , то

4) Объем тела V равен

(2 )

Вычисление тройного интеграла в декартовых координатах.

Пусть D  проекция тела V на плоскость xOy , поверхности z =φ 1 (x , y ), z =φ 2 (x , y ) ограничивают тело V снизу и сверху соответственно. Это значит, что

V = {(x , y , z ): (x , y )D , φ 1 (x , y ) ≤ z ≤ φ 2 (x , y )}.

Такое тело назовем z -цилиндрическим. Тройной интеграл (1) по z -цилиндрическому телу V вычисляется переходом к повторному интегралу, состоящему из двойного и определенного интегралов:

(3 )

В этом повторном интеграле сначала вычисляется внутренний определенный интеграл по переменной z , при этом x , y считаются постоянными. Затем вычисляется двойной интеграл от полученной функции по области D .

Если V  x- цилиндрическое или y- цилиндрическое тело, то верны соответственно формулы

В первой формуле D  проекция тела V на координатную плоскость yOz , а во второй  на плоскость xOz

Примеры. 1) Вычислитьобъем тела V , ограниченного поверхностями z = 0, x 2 + y 2 = 4, z = x 2 + y 2 .

Решение. Вычислим объём при помощи тройного интеграла по формуле (2)

Перейдем к повторному интегралу по формуле (3).

Пусть D  круг x 2 + y 2 ≤ 4, φ 1 (x , y ) = 0, φ 2 (x , y )= x 2 + y 2 . Тогда по формуле (3) получим

Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество

D r = { (r , φ ) : 0 ≤ φ < 2 π , 0 ≤ r ≤ 2} .

2) Тело V ограничено поверхностямиz=y , z= –y , x= 0 , x= 2, y= 1. Вычислить

Плоскости z = y , z = –y ограничиваюттелосоответственно снизу и сверху, плоскости x= 0 , x= 2 ограничивают тело соответственно сзади и спереди, а плоскость y= 1 ограничиваетсправа. V – z- цилиндрическое тело, его проекцией D на плоскость хОу является прямоугольник ОАВС . Положим φ 1 (x , y ) = –y